Leitergraph

Die Leitergraphen $L_{1}$ , $L_{2}$ , $L_{3}$ , $L_{4}$ und $L_{5}$

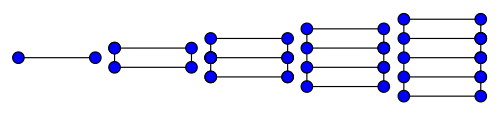
Ein Leitergraph (englisch ladder graph) ist in der Graphentheorie eine Klasse von Graphen mit der Struktur einer Leiter. Ein Leitergraph besteht aus zwei linearen Graphen gleicher Länge (die Holme), wobei je zwei einander entsprechende Knoten durch eine Kante (die Sprossen) miteinander verbunden sind. Jeder Leitergraph ist das kartesische Produkt zweier linearer Graphen, von denen einer genau eine Kante hat, und damit ein spezieller Gittergraph.

Definition

Ein Leitergraph $L_{n}$ ist ein ungerichteter Graph $(V,E)$ bestehend aus den $2n$ Knoten

$V=\{v_{1},\ldots ,v_{2n}\}$

und den $3n-2$ Kanten

$E=\{\{v_{i},v_{i+1}\}\mid i=1,3,\ldots ,2n-1\}\cup \{\{v_{i},v_{i+2}\}\mid i=1,2,\ldots ,2n-2\}$ .

Eigenschaften

2-Färbung eines Leitergraphen

Ein Leitergraph $L_{n}$ ist das kartesische Produkt

$L_{n}=P_{2}\times P_{n}$

der beiden linearen Graphen $P_{2}$ und $P_{n}$ und damit ein spezieller Gittergraph $G_{2,n}$ .

Weitere Eigenschaften sind:

Alle Leitergraphen sind zusammenhängend, planar und bipartit. Für $n\geq 2$ sind alle Leitergraphen auch zyklisch und hamiltonsch.
Bis auf die vier Eckknoten mit Grad zwei weisen alle Knoten eines Leitergraphen den Grad drei auf.
Der Durchmesser und die Stabilitätszahl des Leitergraphen $L_{n}$ beträgt jeweils $n$
Die chromatische Zahl des Leitergraphen $L_{n}$ ist zwei und sein chromatisches Polynom ist $(\lambda -1)\lambda (\lambda ^{2}-3\lambda +3)^{n-1}$ .
Die Anzahl der perfekten Matchings in dem Leitergraphen $L_{n}$ ist gleich der Fibonacci-Zahl $f_{n+1}$ .^[1]

Zyklische Erweiterungen

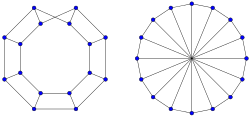
Zwei Ansichten eines Möbius-Leitergraphen

Werden in einem Leitergraphen zudem der erste und der vorletzte sowie der zweite und der letzte Knoten jeweils durch eine zusätzliche Kante miteinander verbunden, bildet man also

$E'=E\cup \{\{v_{1},v_{2n-1}\},\{v_{2},v_{2n}\}\}$ ,

dann erhält man einen zyklischen Leitergraph ( $CL_{n}$ . Ein zyklischer Leitergraph ist das kartesische Produkt $P_{2}\times C_{n}$ eines linearen Graphen mit einem Kreisgraphen $C_{n}$ und damit für $n\geq 2$ 3-regulär. Zyklische Leitergraphen sind die Polyedergraphen von Prismen und werden daher auch Prismengraphen (englisch prism graphs) genannt.

Werden die vier Knoten stattdessen kreuzweise miteinander verbunden, bildet man also

$E'=E\cup \{\{v_{1},v_{2n}\},\{v_{2},v_{2n-1}\}\}$ ,

erhält man als Graph einen sogenannten Möbiusleitergraph (englisch Möbius ladder graph) $ML_{n}$ , der an ein Möbiusband erinnert und ebenfalls 3-regulär ist. Möbiusleitergraphen sind für $n\geq 3$ nicht mehr planar und weisen einige interessante graphentheoretische Eigenschaften auf.^[2]

Siehe auch

Sterngraph

Weblinks

Eric W. Weisstein: Ladder Graph. In: MathWorld (englisch).

Einzelnachweise

↑ Ralph Grimaldi: Fibonacci and Catalan Numbers: An Introduction. John Wiley & Sons, 2012, ISBN 1-118-15976-4, S. 64.
↑ Jonathan L. Gross: Combinatorial Methods With Computer Applications (= Discrete Mathematics and its Applications. Band 54). CRC Press, 2008, ISBN 1-58488-743-5, S. 376–377.

Basierend auf einem Artikel in:

Wikipedia.de