Bateman-Funktion

→ Hauptartikel: Bateman-Gleichung

Menge der Isotope in der Zerfallsreihe 241Pu als Funktion der Zeit

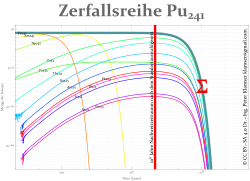
In der Kernphysik ist die Bateman-Funktion die Lösung für das mathematische Modell einer radioaktiver Zerfallsreihe als gekoppelte gewöhnliche Differentialgleichungen, das die Menge $N_{t}$ und Aktivitäten in einer Zerfallskette als Funktion der Zeit $t$ beschreibt.

Die Parameter sind

die Anzahl der Isotope ( $decaysteps$ ), für die die Berechnung durchgeführt werden soll,
die Anzahl der Zerfallsprodukte, für die die Menge $N$ zum Zeitpunkt $t$ (eben $N_{t}$ ) berechnet werden soll,
die Zerfallsraten (Halbwertszeit) $\lambda [i]$ der einzelnen Isotope $i$ oder $j$ in der Zerfallskette,
die anfänglichen Menge an Isotopen $N_{t=0}$ und die Menge $N_{t}$ an Isotopen zum Zeitpunkt $t$ ,
$a[j]$ die Häufigkeit für eine Zerfallsart (branching ratio) (z. B. $\alpha$ - oder $\beta$ -Zerfall, wenn es denn alternative Wege in der Zerfallskette gibt).

Das Modell wurde 1905 von Ernest Rutherford formuliert und die analytische Lösung wurde 1910 von Harry Bateman bereitgestellt.

$N_{t}=\sum _{i=1}^{decaysteps}N_{t=0}[i]\left(\prod _{j=1}^{{decaysteps}-1}{a[j]\lambda }[j]\right)\sum _{j=1}^{decaysteps}{\frac {\mathrm {e} ^{t(-{\lambda }[j])}}{\prod _{n=1}^{decaysteps}{If}[n\neq j,{\lambda }[n]-{\lambda }[j],1]}}$

Die Bateman-Lösung für die gekoppelte Differentialgleichung für exponentielle Zerfallsprozesse wird auch verwendet, um (bio-)chemische oder pharmazeutische Abbauprozesse (auch in der Medizin) quantitativ zu beschreiben.

Bateman-Funktion in der Pharmazie

Graph der Bateman-Funktion Blutplasma

Die Bateman-Funktion ist eine mathematische Beziehung, die ein vereinfachtes Modell der Aufnahme (Invasion) oder Bildung und Elimination eines Stoffes (meist eines Arzneistoffs oder eines Zwischenprodukt in einer radioaktiven Zerfallsreihe) in Abhängigkeit von der Zeit beschreibt. Bei der Bateman-Funktion wird angenommen, dass der Stoff sich in nur einem Kompartiment verteilt und die Aufnahme und Elimination einer Reaktion erster Ordnung folgt. Sie enthält daher zwei exponentielle Terme, die voraussetzen, dass Aufnahme und Elimination nur von der Stoffkonzentration $c$ und damit von der Diffusionskonstanten abhängt. Aktive Prozesse zum Stofftransport oder die unterschiedliche Verteilung und Anreicherung z. B. durch die Hydrophobie des Stoffes bleiben unberücksichtigt. Die Bateman-Funktion wird verwendet, um beispielsweise den Zeitpunkt und die Höhe der maximalen Stoffkonzentration oder das Unterschreiten einer minimalen Wirkkonzentration abzuschätzen. Sie ist nach dem britischen Mathematiker Harry Bateman (1882–1946) benannt. Eine Variante der Bateman-Funktion lautet:

$c(t)=f\cdot {\frac {D}{V}}\cdot {\frac {k_{\mathrm {a} }}{k_{\mathrm {a} }-k_{\mathrm {e} }}}\cdot \left(\mathrm {e} ^{-k_{\mathrm {e} }\cdot t}-\mathrm {e} ^{-k_{\mathrm {a} }\cdot t}\right)$

Dabei bezeichnet $k_{\mathrm {a} }$ die Absorptionsrate, $k_{\mathrm {e} }$ die Eliminationsrate, $D$ die Dosis, $V$ das Verteilungsvolumen und $f$ die Bioverfügbarkeit.

Literatur

Harry Bateman: Solution of a System of Differential Equations Occurring in the Theory of Radioactive Transformations. In: Proc. Cambridge Phil. Soc. Band 15, 1910, S. 423–427.
E. R. Garrett: The Bateman function revisited: a critical reevaluation of the quantitative expressions to characterize concentrations in the one compartment body model as a function of time with first-order invasion and first-order elimination. In: J Pharmacokinet Biopharm. (1994) 22(2): S. 103–128, PMID 7815308
E. R. Garrett: Simplified methods for the evaluation of the parameters of the time course of plasma concentration in the one-compartment body model with first-order invasion and first-order drug elimination including methods for ascertaining when such rate constants are equal. In: J Pharmacokinet Biopharm. (1993) 21(6): S. 689–734, PMID 8138893
Bauer, Frömming, Führer: Lehrbuch der pharmazeutischen Technologie
Langguth, Fricker, Wunderli-Allenspach: Biopharmazie
J. Gabrielsson, D. Weiner: Pharmacokinetic & Pharmacodynamic Data Analysis: Concepts and Applications

Basierend auf einem Artikel in:

Wikipedia.de