Stern-Doppelschicht

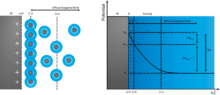
Stern-Modell der elektrochemischen Doppelschicht: M = Elektrodenmetall, ä.H. = äußere Helmholtzfläche, a/2 = Radius der solvatisierten Ionen, x = Entfernung zur Metalloberfläche, Δφ = Potentialunterschied, ζ = Ortskoordinate mit ζ = x − a/2

Die Stern-Doppelschicht ist eine Doppelschicht, die im Elektrolyten durch zwei Bereiche beschrieben wird:

die starre Schicht aus Ionen, die an der Elektrode anliegen (und eventuell solvatisiert sind)
die diffuse Schicht, die daran angrenzt und weit in den Elektrolyten hineinreicht.

Nach der Theorie, die Otto Stern 1924 veröffentlichte^[1], baut sich bei dieser Ladungsverteilung ein Potential auf, das in der starren Schicht linear und in der diffusen Schicht exponentiell ab- oder zunimmt.

Das Modell der Stern-Doppelschicht kombiniert die früheren Modelle der Helmholtzschicht und der Gouy-Chapman-Doppelschicht.^[2]

Potentialverlauf

Die Berechnung des Potentialverlaufs verläuft analog zur Berechnung im Rahmen der Debye-Hückel-Theorie. Man benutzt vorteilhaft die Ortskoordinate^[2]

${\begin{aligned}\zeta &=x-d\\&=x-{\frac {a}{2}}\end{aligned}}$

mit

dem Abstand $x$ von der Elektrodenoberfläche
dem Radius $a$ des Ions.

Der Potentialverlauf im diffusen Teil der Doppelschicht wird dann beschrieben durch die Gleichung^[2]

$\varphi (\zeta )-\varphi _{L}=(\varphi _{aH}-\varphi _{L})\cdot e^{-\zeta /\beta }$

mit

der „Dicke“ $\beta$ der diffusen Doppelschicht (genauer: die Entfernung, bei der das Potential auf den 1/e-ten Teil abfällt). $\beta =\kappa ^{-1}$ ist identisch mit dem in der Debye-Hückel-Theorie definierten „Radius der Ionenwolke“.
dem Potential $\varphi _{L}$ im Inneren des Elektrolyten und
dem Potential $\varphi _{aH}$ für $\zeta =0$ .

Insgesamt erhält man damit für den Potentialverlauf in der gesamten Doppelschicht gemäß dem Stern-Modell:

${\varphi (x)={\begin{cases}\varphi _{M}&{\text{für }}x\leq 0\\\varphi _{M}-(\varphi _{M}-\varphi _{aH})\cdot {\dfrac {x}{d}}&{\text{für }}0\leq x\leq d\\\varphi _{L}+(\varphi _{aH}-\varphi _{L})\cdot e^{-(x-d)/\beta }&{\text{für }}x\geq d\\\varphi _{L}&{\text{für }}x\rightarrow \infty \end{cases}}}$

Einzelnachweise

[Bearbeiten | Quelltext bearbeiten]

↑ Otto Stern: Zur Theorie der elektrolytischen Doppelschicht. In: Deutsche Bunsen-Gesellschaft für Angewandte Physikalische Chemie, Erich Müller (Hrsg.): Zeitschrift für Elektrochemie. Band 30, Nr. 21‐22. Wiley‐VCH Verlag, November 1924, ISSN 0372-8323, S. 508–516, doi:10.1002/bbpc.192400182 (Online [PDF; 5,5 MB; abgerufen am 10. September 2021] bei der Electrochemical Science and Technology Information Resource (ESTIR) der Electrochemical Society).
↑ ^{Hochspringen nach: a} ^b ^c Gerd Wedler: Lehrbuch der Physikalischen Chemie. 5. Auflage. Wiley-VCH, Weinheim 2004, ISBN 3-527-31066-5, 2.7.7 Die elektrischen Doppelschichten, S. 435–440.

Basierend auf einem Artikel in:

Wikipedia.de